EXERCÍCIOS DE LOGARITMO MAIS AVANÇADOS II COM RESOLUÇÃO

    1.       Calcule o valor de x na equação 1000^0,3 = x sabendo que o log 2 = 0,3.

a)       2

b)      4

c)       6

d)      8

e)      10

     2.       O valor aproximado de log₂ 30 fica entre

a)       1 e 2

b)      2 e 3

c)       3 e 4

d)      4 e 5

e)      5 e 6

     3.       Calcule o valor de x / y na equação 40^x = 30^y, considere que o

log 2 = 0,3 e o log 3 = 0,5.

a)       1

b)      1,5 / 2

c)       1,5 / 1,6

d)      1,6 / 1,5

e)      2 / 1,6

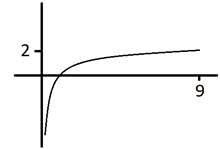
     4.       A representação abaixo representa a função f(x) = log_a (x)

Assinale a alternativa que representa a solução de log_a (a² + 18)

a)       1

b)      2

c)       3

d)      4

e)      5

RESOLUÇÃO

    1.       Primeiro vamos transformar o 1000 em base 10

1000 = 10³

Agora vamos voltar para a equação

10^{3 . 0,3} = x

Vamos aplicar log

Log₁₀­ x = 3 . 0,3

Vamos substituir o 0,3 por log₁₀ 2

Log₁₀ x = 3 . log₁₀ 2

Vamos voltar com o 3 da frente do log de 2 para expoente

Log₁₀ x = log₁₀ 2³

Agora podemos eliminar os dois log

X = 2³

X = 8

    2.       Primeiro vamos resolver o log

2^x = 30

Então vamos tentar descobrir qual expoente poderia servir para transformar o 2 em um número próximo de 30

2¹ = 2

2² = 4

2³ = 8

2⁴ = 16

2⁵ = 32

Como o trinta fica entre 16 e 32, o valor fica entre 4 e 5.

    3.       Como temos uma igualdade, vamos aplicar o log nos dois lados da igualdade

Log 40^x = log 30^y

Jogue o expoente para frente do log

X . log 40 = y . log 30

Agora transforme 40 e 30, pois como foi dado o valor de log de 2 e 3, devemos encontrar dois e três.

X . log 4 . 10 = y . log 3 . 10

X . (log 2² + log 10) = y . (log 3 + log 10)

X . (2 . log 2 + 1) = y . (log 3 + 1)

X . (2 . 0,3 + 1) = y . (0,5 + 1)

X . (0,6 + 1) = y . (1,5)

1,6 x = 1,5 y

x/y = 1,5 / 1,6

    4.       Primeiro devemos pegar um ponto onde temos x e y, este ponto é x = 9 e y = 2, agora podemos aplicar na fórmula dada

Log_a x = y

Log_a 9 = 2

a² = 9

a² = 3²

a = 3

como descobrimos o valor de a, podemos agora aplicar na outra fórmula

log_a (a² + 18)

log₃ (3² + 18)

log₃ (9 + 18)

log₃ (27)

3^x = 27

3^x = 3³

X = 3