Exercícios sobre polinômios e suas raízes

Polinômios

1. Descubra as possíveis raízes das equações abaixo

a) x³ - 3x² – 4x + 12

b) x³ – 2x² – x + 2

c) x⁴ – 4x³ – x² + 16 x – 12

d) x³ – 5x² – x + 5

e) x³ – 6x² + 11x – 6

2. Quais as raízes dos polinômios abaixo

a) x⁴ – 5x² + 4

b) x⁴ + x³ – 7x² – x + 6

c) x³ – 9x² + 26x – 24

d) x³ – 7x² – x + 7

e) x³ + 2x² – x – 2

3. Qual a soma das raízes de cada polinômio abaixo

a) x³ – 4x² + x + 6

b) x³ – x² – 4x + 4

c) x³ – 6x² – x +6

d) x⁴ – 6x³ – x² + 54x – 72

e) x⁴ – 11x³ + 41x² – 61x + 30

4. Calcule o produto das raízes de cada polinômio abaixo

a) x³ + 3x² – 4x – 12

b) x³ – x² – 25x + 25

c) x³ – x²/2 – x + ½

d) x³ + 9x²/2 – 17x/2 + 3

e) x³ – x² – 14x + 24

GABARITO

1

    A)     ±1, ±2, ±3, ±4, ±12 

    B)      ±1, ±2

    C)      ±1, ±2, ±3, ±4, ±6, ±12

    D)     ±1, ±5

    E)      ±1, ±2, ±3, ±6

2

   A)     1, -1, 2, -2

   B)      1, -1, -2, 3

   C)      2, 3, 4

   D)     1, -1, 7

   E)      1, -1, -2

3 

   A)     +4

   B)      +1

   C)      +6

   D)     +6

   E)      +11

4

   A)     +12

   B)      -25

   C)      -1/2

   D)     -3

   E)      -24

Exercícios de polinômios, divisão e raízes

     1.       Faça as divisões dos polinômios.

a)      X⁴ + x³ – 7x² + 9x – 1    /   x² + 3x – 2

b)      X² + 4x + 3     /     x + 1

c)       X³ + x² – x + 1    /     x + 4

d)      X⁴ – 10x³ + 24x² + 10x – 24   /    x² – 6x + 5

e)      5x² – 3x + 2    /    x + 3

f)       X⁴ + 3x² + x – 5     /     x + 2

      2.       Descubra as raízes dos polinômios

a)      x³ – 2x² – x + 2

b)      x³ – x² – 4x + 4

c)       2x⁴ – 3x³ + 3x – 2

d)      x⁴ – 4x³ – 7x² + 16x – 12

RESPOSTAS.

Questão 1:

     a)      x² – 2x + 1, resto 2x + 1

     b)      x + 3

     c)       x² – 3x + 11, resto -47

     d)      x² – 4x – 5, resto 1

     e)      5x – 18, resto 56

     f)       x³ – 2x² + 7x + 15, resto 35

Questão 2:

    a)      R {1, 2, -1}

    b)      R {1, 2, -2}

    c)       R {1, - 1, 2, 1/2}

    d)      R {1, - 2, 2, -3}

Exercícios sobre polinômios para a UFRGS

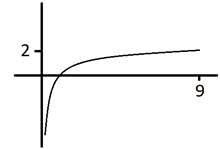
1.      Na figura a seguir, temos um esboço de parte do gráfico de uma função polinomial

Analise as seguintes afirmativas:

(     ) O grau do polinômio p(x) é ≤ 6.

(     ) O grau do polinômio p(x) é ≥ 7.

(     ) A equação p(x) = 0 não possui raízes reais.

(     ) O polinômio p(x) é divisível por x(x+2)(x-2).

(     ) O polinômio p(x) é divisível por (x²-1)(x-3)(x-4).

 

2. (Mackenzie) Se k e p são, respectivamente, a soma e o produto das raízes da equação 4x⁴-2x³+x² - x+1=0, então k+p vale:

a) -4

b) -2/5

c) +1/4

d) -1/4

e) 5/2

3. (Uel) O polinômio x¤ - x£ - 14x + 24 é divisível por

a) x - 1  e  x + 3

b) x - 2  e  x + 5

c) x - 2  e  x + 4

d) x - 3  e  x + 2

e) x + 5  e  x – 3

4. (Uel) A equação 2x³ - 5x² + x + 2 = 0 tem três raízes reais. Uma delas é 1. As outras duas são tais que

a) ambas são números inteiros.

b) ambas são números negativos.

c) estão compreendidas entre -1 e 1.

d) uma é o oposto do inverso da outra.

e) uma é a terça parte da outra.

5. (Unaerp) Se P(x) = 3x³ - 5x² + 6x + a  é divisível por x - 2, então os valores de a e de P(2), são respectivamente:

a) - 16 e - 2

b) - 16 e 2

c) 16 e - 2

d) 16 e 2

e) - 16 e zero

6. (Fatec) Se -1 é raiz do polinômio p(x)= x³- 4x² + x - k, kᴁ IR, então as outras duas raízes são

a) reais e de multiplicidade 2.

b) racionais e negativas.

c) não reais.

d) irracionais.

e) inteiras.

7. (Fuvest) O gráfico

pode representar a função f(x) =

a) x (x - 1)

b) x² (x² - 1)

c) x³ (x - 1)

d) x (x² - 1)

e) x² (x - 1)

8. (Uerj) A figura a seguir representa o polinômio P definido por P(x)=x¤-4x.

a)      Determine as raízes desse polinômio.

9. (Puccamp) Sabe-se que o polinômio f = x⁴ +4x³ +8x² +16x+16 admite a raiz -2 com multiplicidade 2. As demais raízes desse polinômio são números

a) inteiros e opostos.

b) racionais não inteiros.

c) irracionais e positivos.

d) irracionais e opostos.

e) não reais.

10. (Ufscar) Sabendo-se que a soma de duas das raízes da equação x³-7x² +14x-8=0 é igual a 5, pode-se afirmar a respeito das raízes que

a) são todas iguais e não nulas.

b) somente uma raiz é nula.

c) as raízes constituem uma progressão geométrica.

d) as raízes constituem uma progressão aritmética.

e) nenhuma raiz é real.

11. (Fatec) A equação 4x⁴ -24x³ +45x² -29x+6=0 tem duas raízes que são números inteiros, os quais, como se sabe, devem ser divisores do termo independente. A soma das raízes não inteiras dessa equação é

a) 0

b) 1/4

c) 1

d) 2 √2

e) 5,25

12. (Uel) A multiplicidade da raiz 1 na equação 

X⁵ - 8x⁴ + 24x³ - 34x² + 23x - 6 = 0    é 

a) 0

b) 1

c) 2

d) 3

e) 4

13. (Pucrs) Na figura, tem-se o gráfico de p(x)=ax³ +bx² +cx+d. Os valores de a, b, c e d são respectivamente,

a) -4, 0, 4 e 2

b) -4, 0, 2 e 4

c) 1/4, 2, 10 e 4

d) 1/4, 0, -3, e 4  

e) 1, 0, -12 e 16

GABARITO

1 – F, V, F, V, V

2 – D

3 – C

4 – D

5 – E

6 – E

7 – D

8 – {-2, 0, 2}

9 – E

10 – C

11 – C

12 – D

13 – D

Exercícios sobre polinômios

1. (Unitau) Sabe-se que 1, 2 e 3 são raízes de um polinômio do terceiro grau P(x) e que P(0)=1. logo, P(10) vale:

a) 48.

b) 24.

c) - 84.

d) 104.

e) 34.

R: c

2. (Uel) A equação 2x³ - 5x² + x + 2 = 0 tem três raízes reais. Uma delas é 1. As outras duas são tais que

a) ambas são números inteiros.

b) ambas são números negativos.

c) estão compreendidas entre -1 e 1.

d) uma é o oposto do inverso da outra.

e) uma é a terça parte da outra.

R: d

3. (Fatec) Se -1 é raiz do polinômio p(x)= x³- 4x²+ x - k, k ЄIR, então as outras duas raízes são

a) reais e de multiplicidade 2.

b) racionais e negativas.

c) não reais.

d) irracionais

R: e

4. (Uel) Na divisão de x⁵+2x⁴-3x³+x²-3x+2 por x²+x+1, o

a) quociente é x³+x²-5x+5

b) resto é 8x+3

c) quociente é x³+x²+x+1

d) resto 3x+8

e) quociente é x³+5x²-x+5

R: a

5. (Fuvest) O gráfico

pode representar a função f(x) = a) x (x - 1)

b) x² (x² - 1)

c) x³ (x - 1)

d) x (x² - 1)

e) x² (x - 1)

R: d

6. (Uel) Sabe-se que a equação: 2x⁶ + 11x⁵ + 20x⁴ + 15x³ + 10x+² + 4x - 8 = 0, admite a raiz -2 com multiplicidade 3. Sobre as demais raízes dessa equação é correto afirmar que

a) são números racionais.

 b) são números irracionais.

c) são números não reais.

d) duas são não reais e uma é racional.

e) duas são irracionais e uma é racional.

R: d

7. (Ufal) Sabe-se que as raízes da equação 2x³+x²- 7x-6=0 são diretamente proporcionais aos números 3, 2 e -4. Nessas condições, a menor das raízes é

a) -3

b) -2

c) -3/2

d) -1

e) -1/2

R: c

8. (Ufrs) Dentre os gráficos abaixo, o único que pode representar o polinômio p(x) = x³ + kx² + x , sendo k uma constante real, é

R: e

9. (Pucrs) Na figura, tem-se o gráfico de p(x)=ax³+bx²+cx+d. Os valores de a, b, c e d são respectivamente,

a) -4, 0, 4 e 2

b) -4, 0, 2 e 4

c) 1/4, 2, 10 e 4

d) 1/4, 0, -3, e 4

e) 1, 0, -12 e 16

R: d

EXERCÍCIOS SOBRE TITULAÇÃO COM RESOLUÇÃO

1. Uma solução de NaOH foi preparada com 20 g da base em 500 ml de água, outra solução de H₂S foi preparada com 34 g do acido em 500 ml de água. Qual o volume de ácido será necessário para neutralizar completamente 100 ml da base?

2. Qual o volume necessário de Ca(OH)₂ 0,1 M será necessário para neutralizar completamente uma solução de 20 mL de H₂SO₄ 0,1 M.

3. Uma solução de Al(OH)₃ preparada com 91 mg da base em 100 mL de água será neutralizada com uma solução de HCl que foi preparada com 365 mg em 100 mL de água. Qual o volume do ácido será necessário para neutralizar completamente o volume da base.

4. 10 mL de Mg(OH)₂ de 0,5 M foi neutralizado por 2 mL de H₃PO₄, qual a concentração do ácido?

5. 20 mL de H₂S 0,1 M foi neutralizado com um determinado volume de Pb(OH)₄ 0,5 M, qual foi o volume de base utilizado?

GABARITO

a) Primeiramente devemos cacular a concentração da base e do ácido em mol . L^-1.

Mol  L^-1 da base

Agora vamos cacular a concentração em mol . L^-1 para o ácido

Vamos fazer a fórmula da titulação, mas cuidando o número de hidroxilas da base e o número de hidrogênios do ácido, que devem multiplicar a concentração em cada um dos casos.

25 mL

b)Vamos aplicar a fórmula da titulação, mas sempre cuidando o número de hidrogênios e hidroxilas

V_b 20 mL

3) Primeiro vamos calcular a concentração em mol . L^-1 de cada um deles, iniciarei pela base

Agora vamos para o ácido.

Agora vamos aplicar na fórmula da titulação, não esqueça de colocar o número de hidrogênios e hidroxilas.

4) Como já é dado a concentração e os volumes, vamos direto para a fórmula da titulação, sem esquecer da quantidade de hidrogênio e hidroxilas.

5) Como já é dados as concentrações, vamos direto para a fórmula da titulação, sem esquecer a quantidade de hidroxila e hidrogênio.

Resolução dos exercícios de hidrostática

EXERCÍCIOS DE LOGARITMO MAIS AVANÇADOS II COM RESOLUÇÃO

    1.       Calcule o valor de x na equação 1000^0,3 = x sabendo que o log 2 = 0,3.

a)       2

b)      4

c)       6

d)      8

e)      10

     2.       O valor aproximado de log₂ 30 fica entre

a)       1 e 2

b)      2 e 3

c)       3 e 4

d)      4 e 5

e)      5 e 6

     3.       Calcule o valor de x / y na equação 40^x = 30^y, considere que o

log 2 = 0,3 e o log 3 = 0,5.

a)       1

b)      1,5 / 2

c)       1,5 / 1,6

d)      1,6 / 1,5

e)      2 / 1,6

     4.       A representação abaixo representa a função f(x) = log_a (x)

Assinale a alternativa que representa a solução de log_a (a² + 18)

a)       1

b)      2

c)       3

d)      4

e)      5

RESOLUÇÃO

    1.       Primeiro vamos transformar o 1000 em base 10

1000 = 10³

Agora vamos voltar para a equação

10^{3 . 0,3} = x

Vamos aplicar log

Log₁₀­ x = 3 . 0,3

Vamos substituir o 0,3 por log₁₀ 2

Log₁₀ x = 3 . log₁₀ 2

Vamos voltar com o 3 da frente do log de 2 para expoente

Log₁₀ x = log₁₀ 2³

Agora podemos eliminar os dois log

X = 2³

X = 8

    2.       Primeiro vamos resolver o log

2^x = 30

Então vamos tentar descobrir qual expoente poderia servir para transformar o 2 em um número próximo de 30

2¹ = 2

2² = 4

2³ = 8

2⁴ = 16

2⁵ = 32

Como o trinta fica entre 16 e 32, o valor fica entre 4 e 5.

    3.       Como temos uma igualdade, vamos aplicar o log nos dois lados da igualdade

Log 40^x = log 30^y

Jogue o expoente para frente do log

X . log 40 = y . log 30

Agora transforme 40 e 30, pois como foi dado o valor de log de 2 e 3, devemos encontrar dois e três.

X . log 4 . 10 = y . log 3 . 10

X . (log 2² + log 10) = y . (log 3 + log 10)

X . (2 . log 2 + 1) = y . (log 3 + 1)

X . (2 . 0,3 + 1) = y . (0,5 + 1)

X . (0,6 + 1) = y . (1,5)

1,6 x = 1,5 y

x/y = 1,5 / 1,6

    4.       Primeiro devemos pegar um ponto onde temos x e y, este ponto é x = 9 e y = 2, agora podemos aplicar na fórmula dada

Log_a x = y

Log_a 9 = 2

a² = 9

a² = 3²

a = 3

como descobrimos o valor de a, podemos agora aplicar na outra fórmula

log_a (a² + 18)

log₃ (3² + 18)

log₃ (9 + 18)

log₃ (27)

3^x = 27

3^x = 3³

X = 3

EXERCÍCIOS SOBRE LOGARITMO MAIS APROFUNDADOS

    1.       Analisando o gráfico abaixo, descubra o valor de a em f(x) = log _a x

     2.       Sabendo que log 2 = 0,3, resolva log₂ 400²

    3.       Calcule o valor de x na equação 50^x = 100, sabendo que log 2 = 0,3

    

    

   4.       Calcule o valor de log₄ x^y se log₂ 4 = x e log₅ 625 = y

    Resolução

1. 

primeiro devemos analisar um ponto no gráfico, no caso é o ponto (4, 2) onde x = 4 e y = 2

Agora vamos substituir f(x) por y (2) e x por 4

2 = log _a 4

Vamos resolver o log

a² = 4

a² = 2²

a = 2

2. 

Vamos resolver o log por partes

2 . log₂ 400

2 . log₂ 100 . 4

2 . log₂ 10² . 2²

2 . (log₂ 10² + log₂ 2²)

2 . (2.log₂ 10 + 2. log₂ 2)

2 . (2 . [log₂ 10 + log₂ 2])

4 . [log 10 + 1]

       log 2

4 . [  1  + 1]

       0,3

4 . [  1  +  0,3]

            0,3

4 . 1,3

     0,3

5,2

0,3

3. 

Resolvendo, devemos transformar 50^x = 100 em log

log₅₀ 100 = x

Agora vamos resolver o log

log 100 = x

log 50

log 10² =

log 100/2

    2 log 10         = x

log 100 – log 2

          2 x 1         = x

   log 10² – 0,3

             2           = x

2 log 10 – 0,3

           2           = x

  2 x 1 – 0,3

    2      = x

2 – 0,3

  2  = x

1,7

4. 

primeiro vamos resolver log₂ 4  e depois log₅ 625

log₂ 4 = x

log₂ 2² = x

2 . log₂2 = x

2 . 1 = x

x = 2

log₅ 625 = y 

log₅ 5⁴

4 log₅ 5 = y

4 . 1 = y

 y = 4

Agora vamos montar o log proposto

log₄ 2⁴

log₄ 16

log₄ 4²

2 log₄ 4

2 . 1 = 2

EXERCÍCIOS DE CÁLCULO DE MASSA PRECIPITADA COM GABARITO

CÁLCULO DE MASSA PRECIPITADA

1. Qual a massa precipitada de Na₂O se uma solução for preparada com 20 g deste soluto em 100 ml de água, considerando que o coeficiente de solubilidade dele seja de 0,15 g/ml.

2. Qual a massa precipitada de FeCl₂ se uma solução for preparar com 350 g deste soluto em 700 ml de água, considerando que o seu coeficiente de solubilidade seja de 0,4 g/ml.

3. Qual a massa precipitada de CaO se uma solução for preparada com 50 g deste soluto em 150 ml de água, considerando que o seu coeficiente de solubilidade seja de 0,4 g/ml.

4. Qual a massa de precipitado que se forma quando uma solução é preparada com 100 g de CaS em 200 ml de água se o seu coeficiente de solubilidade for de 0,4 g/ml.

5. Qual a quantidade de máxima de massa de KOH ainda pode ser colocada em uma solução, que apresenta uma concentração de 0,3 g/ml, que apresenta um volume de 100 ml se o seu coeficiente de solubilidade for de 0,5 g/ml.

GABARITO

1 – 5 g.

2 – 70 g.

3 – não ocorre precipitado.

4 – 20 g.

5 – 20 g.

EXERCÍCIOS COM GABARITO DE CONCENTRAÇÃO COMUM

1.Calcule a concentração, em g/ml, de uma solução preparada com 200 ml de água e 20 g de NaCl.

2. Calcule a concentração, em g/ml, de uma solução preparada com 500 ml de água e 40 g de CaO.

3. Calcule a concentração, em kg/L, de uma solução preparada com 300 g de NaCl em 2 L.

4. Calcule a concentração, em kg/L, de uma solução preparada com 2 kg de CaO em 4000 ml.

5. Qual a massa necessária de KI para preparar uma solução de 200 ml, com concentração 2 g/ml.

6. Qual a massa necessária de Fe(OH)₂ para preparar uma solução de 2 L, com concentração de 0,5 g/ml.

7. Qual a massa necessária de HCl para preparar uma solução de 500 ml, com concentração de 1,5 kg/L.

8. Qual o volume de água necessário para preparar uma solução de HI com concentração de 0,4 g/ml se forem utilizados 30 g de HI.

9. Qual o volume de água necessário para preparar uma solução de MgO com concentração de 0,5 kg/L se forem utilizados 500 g de MgO.

10. Qual a concentração, em g/ml, de uma solução preparada com 0,24 kg de Al₂O₃ em 2,4 L de água.

GABARITO

1 – 0,1 g/ml

2 – 0,8 g/ml

3 – 0,15 kg/L

4 – 0,5 kg/L

5 – 400 g

6 – 1000 g

7 – 0,75 kg

8 – 75 ml

9 – 1 L

10 -  0,1 g/ml