Intersecção de retas e área entre retas - explicações e exercícios

RETOMADA DE EQUAÇÃO DA RETA – ENCONTRO DE RETAS

Para verificar o ponto de encontro das retas devemos inicialmente igualar as retas e depois pegar um dos pontos e colocar um uma reta. Não entendeu, vamos ao exemplo.

Ex 1:

Descubra o ponto de encontro entre as retas A = y + 2 x + 3 = 0 e B = 2 y – 4 x + 6 = 0.

Para começar, devemos formar uma reta em uma função f(x) = ax + b, então devemos isolar a letra y para poder formar a equação da reta, relembrando que f(x) = y.

Agora vamos igualar as fórmulas para descobrir o valor de x

Agora vamos colocar 0 em uma das equações. Eu vou escolher a equação y = 2x – 3, pois o x é positivo, apenas frescura minha!

y = 2 . 0 – 3

y = -3

Então o ponto de encontro entre as duas retas é (0, -3).

Exercícios:

   1.       Duas retas, A = y – 2x + 2 = 0; e B = 2y + 6x – 4 = 0 apresentam um ponto de intersecção, qual é este ponto?

   2.       Qual o ponto de intersecção entre as retas A = y = 3x + 4 e B = y = -2x – 1.

   3.       Qual o ponto de intersecção entre as retas A = y = -2x + 4 e B = y = 3x + 2.

   4.       Analise os gráficos abaixo e encontre o ponto de interseção entre as retas A e B.

5. (Unitau) A equação da reta que passa pelos pontos (3,3) e (6,6) é:

a) y = x.

b) y = 3x.

c) y = 6x.

d) 2y = x.

e) 6y = x.

6. (Cesgranrio) A equação da reta mostrada na figura a seguir é:

a) 3x + 4y - 12 = 0

b) 3x - 4y + 12 = 0

c) 4x + 3y + 12 = 0

d) 4x - 3y - 12 = 0

e) 4x - 3y + 12 = 0

7. Determine o ponto P de intersecção entre retas de equações 2x-5y+3=0 e x-3y-7=0

Agora vamos calcular a área formada pela intersecção entre duas retas e delas com algum dos eixos, x ou y.

Ex 1:

Qual a área formada pela figura formada pela união dos pontos referentes à intersecção entre as retas A) y - 2 x + 4 = 0 e a reta B) - 2 y - 4 x - 6 = 0 e delas com o eixo das abscissas.

Primeiro devemos encontrar os três pontos aos quais o a pergunta se refere, a intersecção das retas e a intersecção delas com o eixo das abscissas. Depois podemos montar o gráfico e ver a figura formada, tentando sempre enxergar triângulos retângulos no gráfico, ou fazer a área de um triângulo com três pontos pela determinante de uma matriz.

1º) intersecção das retas:

Vamos montar as retas no formato y = ax + b

Reta A)

y - 2 x + 4 = 0

y = + 2 x - 4

Reta B)

- 2 y - 4 x - 6 = 0

- 2 y =  4 x + 6

y =  4 x + 6

           -2

y = - 2 x - 3

O dois de baixo deve dividir os dois números de cima, lembrando que ele é negativo então muda o sinal dos números de cima.

Agora vamos igualar as equações para descobrir o valor de x

2 x - 4 = - 2 x - 3

2 x + 2 x = - 3 + 4

4 x = 1

x = 1

      4

Agora colocamos este x em uma das equações para descobrir y, que pode ser a y = 2 x - 4

y = 2 . 1 - 4

           4

y = 2 - 4

       4

y = 1 - 4

      2

y = - 7

        2

Então o ponto de encontro das duas retas é (1/4, -7/2)

Agora vamos descobrir o ponte de intersecção das retas com o eixo das abscissas, para isto devemos colocar 0 no y e descobrir x

A) y = 2 x - 4

0 = 2 x - 4

4 = 2 x

4 / 2 = x

x = 2

Ponto (2, 0)

E agora a outra reta

B) y = - 2 x - 3

0 = - 2 x - 3

2 x = -3

x = -3 / 2

Ponto (-3 / 2, 0)

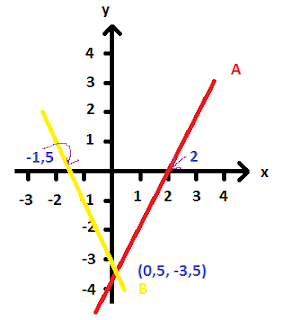
Agora vamos traçar o gráfico

Vamos começar com a reta A, que cruza em y em -4 e cruza em x em 2

Agora vamos montar o gráfico com a reta B, que cruza y em - 3 e x em -3 / 2

Agora vamos colocar os três pontos que são pedidos, o de encontro entre as retas, os de encontro das retas com o eixo das abscissas.

Então a área formada é um triângulo, com  base no valor de 3,5 e altura de 3,5. Mas como assim?

A base vai de -1,5 até 2, resultando em 3,5 e a altura vai de zero até -3,5 (em y), resultando 3,5.

Então agora teremos que resolver a fórmula da área de triângulo

8. (Unesp) Seja A a intersecção das retas r, de equação y=2x, e s, de equação y=4x-2. Se B e C são as intersecções respectivas dessas retas com o eixo das abscissas, a área do triângulo ABC é:

a) 1/2.

b) 1.

c) 2.

d) 3.

e) 4.  

9. (Cesgranrio) A área do triângulo cujos vértices são os pontos (1,2), (3,5) e (4,-1) vale: a) 4,5

b) 6

c) 7,5

d) 9

e) 15

10. Calcule a área do triângulo formado pela intersecção das retas e delas com o eixo das abscissas.

11. Qual a área do quadrilátero formado pela intersecção das retas nos eixos das abscissas e das ordenadas das retas abaixo

A) y = - x - 2

B) y = - x/2 + 2

GABARITO

1 – (4/5, -2/5)

2 – (-1, 1)

3 – (2/5, 16/5)

4 -  A – (10/3, 10/3)

      B – (27/7, 12/7)

      C – (8, 2)

      D – (4, -7)

5 – a

6 – b

7 – (-26, - 49/3)

8 – a

9 – c

10 – 27/10

11 – 12