Retomada de equações exponenciais com gráficos e exercícios

RETOMADA DE EQUAÇÕES EXPONENCIAIS

São equações que apresentam a variável (geralmente x) no expoente.

Formas que pode aparecer:

f(x) = a^x

Neste caso o gráfico é uma crescente e sempre que o x apresentar uma valor de zero, a ordenada (y) será igual a 1.

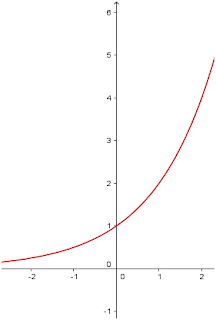
Ex 1:

Vamos analisar o gráfico abaixo e encontrar a equação que o representa.

Para podermos encontrar a equação que representa o gráfico devemos ter dois pontos e analisar que tipo de gráfico estamos observando.

Neste caso, quando x = 0 o valor de y = 1, então é um gráfico do tipo f (x) = a^x, com o outro ponto vamos descobrir o valor de a substituindo x e y na equação. O outro ponto será (1, 3).

Lembrando que f (x) é o valor de y, vamos lá.

f (x) = a^x

3 = a¹

3 = a

Então f(x) = 3^x

Ex2: Qual o gráfico da função f(x) = 2^x

Primeiro vamos analisar o tipo de gráfico que será formado, ele deve ser crescente e passar em y por 1.

Para descobrir que o gráfico passa por 1 em y devemos colocar zero no x.

f(x) = 2⁰ = 1.

Agora vamos colocar outro ponto em x para descobrir onde passa em y.

f(x) = 2¹ = 2.

Então, quando x vale 1 o y vale 2

Agora vamos dar um número negativo para x, como -1.

f(x) = 2^-1

f(x) = ½ = 0,5

Vamos dar outro número positivo para x, como 2

f(x) = 2²

f(x) = 4

Agora vamos montar o gráfico.

Agora vamos analisar equações como f(x) =( ½)^x

Neste caso o gráfico será decrescente, pois é uma fração elevada a um expoente.

Ex 3: Qual o gráfico da função f(x) = (1/3)^x

Inicialmente vamos verificar onde a função cruza em y.

Para verificar devemos colocar x = 0

f(x) = (1/3)⁰

f(x) = 1

Vamos lembrar que quando o expoente for negativo devemos inverter o número.

Agora vamos colocar valores em x positivos e negativos.

f(x) = (1/3)^-2 = 3² = 9

f(x) = (1/3)^-1 = 3¹ = 3

f(x) = (1/3)¹ = 1/3

f(x) = (1/3)² = 1/9

Agora vamos colocar os pontos no gráfico.

Ex 4: Qual o gráfico da função f(x) = 2^-x

O gráfico desta função será igual da função f(x) = (1/2)^x, logo será parecido com o gráfico da questão anterior.

Ex 5: Qual o gráfico da função f(x) = (1/2)^-x

Neste caso a função ficará f(x) = 2^x, então o gráfico ficará como o primeiro, crescente.

Ex 6: Qual o gráfico da função f(x) = 2^x + 2

Quando ocorre uma soma ou subtração na função, devemos saber que o gráfico será deslocado para cima ou para baixo, sendo que o deslocamento será igual ao número somado ou subtraído, como por exemplo nesta questão, que somamos 2, então o gráfico será deslocado 2 números em y para cima. Vamos ver o gráfico de f(x) = 2^x

Agora vamos ver o gráfico deslocado por causa do 2

Agora notamos que o gráfico é o mesmo, mas deslocado 2 valores para cima.

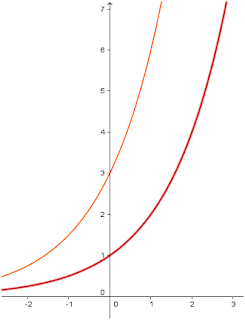
Ex 7: Qual o gráfico de f(x) = 3 . 2^x

Novamente vamos analisar o gráfico de f(x) = 2^x

Agora vamos compreender que quando um valor multiplica ou divide o 2^x, altera a inclinação da curva e a altura dela.

O gráfico em vermelho é da função f(x) = 2^x e o gráfico em vermelho é da função f(x) = 3 . 2^x.

Na comparação podemos verificar que mudou a inclinação e a posição de y quando x = 0.

Ex 8: Vamos comparar o gráfico de f(x) = 2^x, f(x) = 3 . 2^x e f(x) = 2^x + 2

Notamos que no gráfico marrom, ocorreu o deslocamento para cima sem uma mudança brusca na inclinação da reta, então é a função 2^x mais uma soma.

Já na função amarela, notamos que também houve um deslocamento para cima, mas a inclinação mudou bastante, logo temos uma multiplicação.

   Exercícios sobre equações exponenciais

   1.       Cada gráfico abaixo configura uma função exponencial, identifique cada um deles

   2.       Identifique as funções crescentes e as decrescentes.

a)      f(x) = 4^x

b)      f(x) = π^x

c)       f(x) = (√2/2)^x

d)      f(x) = (√3)^x

e)      f(x) = (√3/ 2)^x

f)       f(x) = (0,01)^x

g)      f(x) = (1/5)^x

h)      f(x) = 2^-x

    3.       Resolva as seguintes equações exponenciais com incógnita x

a)      2^x = 64

b)      3 ^{x – 2} = 9

c)       5 ^{x^2 – 2x} = 125

d)      10 ^{1 – x} = 1 / 10

e)      (√2)^x = 4

f)       (0,5)^2x = 2 ^{1 – 3x}

g)      2 ^{4x - x^2} = 8

h)      (10^x)^{1 – x} =0,000001

i)        3 ^{2-  x} = 1 / 27

j)        3 ^{x – 5} = 27 ^{1 – x}

k)      (1/2)^{x^2 – 4} = 8^{x + 2}

l)        ⁵√2^x = 1 / 32

m)    100^{x + 3} = 1 / 10

n)      8^{x – 4} = 4^{x + 1}

o)      9 ^{x – 2} = √27

p)      (1/16)^{x – 2} = 8^x

q)      (0,01)^{x – 1} = 1000

r)       (4^x)^x = 512²

s)       (0,25)^{x – 1} = (1/8)^{1 – x}

t)       25^x/5 = 1

u)      2 . 3^{x – 2} = 162

v)      3 . 5^{x – 1} = 75

w)    5 . 2^{x^2 – 4} = 160

x)      10 . 2^{x + 3} = 10

y)      2^x + 2^{x – 1} = 12

z)       3^{x – 2} + 3^{x + 1} = 84

aa)   7^x + 7^{x – 1} = 8

bb)  4 . 2^x + 2^{x – 1} = 72

cc)    3^2x + 2 . 3^x – 15 = 0

dd)  2^2x – 2 . 2^x – 8 = 0

ee)  3^2x + 3^x = 6

ff)     2^{2x + 1} + 3 . 2^{x + 1} = 8

gg)   4^{x + 2} – 3 . 2^{x + 3} = 160

hh)  3^2x + 2 . 3^x – 15 = 0

ii)       2^{2x + 1} + 3 . 2^{x + 1} = 8

jj)      4^{x + 2} – 3 . 2^{x +3} = 160

kk)   9^x + 3 – 3^x = 0

     4

ll)       3^x – 9 = 8

       3^x

mm)         25^x + 125 = 5^{x + 1}

              6

GABARITO

1 –

a)      f(x) = 2^x

b)      f(x) = (3/2)^x

c)       f(x) = 0,7^x

d)      f(x) = 5^x + 1

e)      f(x) = + 6

a)      6

b)      4

c)       (-1, 3)

d)      2

e)      4

f)       1

g)      (1, 3)

h)      (-2, 3)

i)        5

j)        2

k)      (-2, -1)

l)        -25

m)    (-7/2)

n)      14

o)      11/4

p)      8/7

q)      -1/2

r)       (-3, 3)

s)       1

t)       ½

u)      6

v)      3

w)    (-3, 3)

x)      -3

y)      3

z)       3

aa)   1

bb)  4

cc)    1

dd)  2

ee)  1

ff)     0

gg)   2

hh)  1

ii)       0

jj)      2

kk)   (0, 1)

ll)       2

mm)                    (1, 2)

Exercícios de logaritmo com gabarito parte 1, básico

Exercícios de revisão de logaritmo para fixação da matéria.

   1.       Descubra o valor de cada logaritmo sabendo que log 2 = 0,3 e log 3 = 0,47.

a)      log 20

b)      log 400

c)       log 0,002

d)      log 0,2

e)      log 50

f)       log 25

g)      log 5

h)      log 30

i)        log 900

j)        log 0,03

k)      log 0,3

l)        log 100/3

m)    log 50/3

n)      log 6

o)      log 60

   2.       Agora vamos utilizar a propriedade de mudança de base com as mesmas informações da questão anterior.

a)      log₂10

b)      log₅20

c)       log₃₀40

d)      log₆20

e)      log₅100

f)       log₂₀200

    3.       Para finalizar este procedimento, vamos juntar tudo e tentar resolver algumas questões mais tensas.

a)      3³ = 2^x

b)      20^0,4 = x

c)       Se log₂ x = 2 e log ₆ y = 2, então quanto vale log ₃ y / x

 GABARITO

1.

a) 1,3

b) 2,6

c) – 2,7

d) - 0,7

e) 1,7

f) 1,4

g) 0,7

h) 1,47

i) 2,94

j) -1,53

k) -0.53

l) 1,53

m) 1,23

n) 0,77

o) 1,77

2.

a) 3,33

b) 1,85

c) 1,14

d) 1,85

e) 2,85

f) 1,76

3.

a) 4,7

b) 10^0,52

c) 2

Exercícios de revisão sobre oxi-redução

₀₁₎           (UFMG) Entre as reações indicadas, a única que envolve transferência de elétrons é:
a) AgNO_{3 (aq)} + NaCl_(aq) --> AgCl_(s) + NaNO_3(aq)

b) CaCO_3(s) --> CaO_(s) + CO_2(g)

c) CaO_(s) + H₂O_(l) --> Ca(OH)_2(aq)

d) H₂O_2(l) --> 2H₂O_(l) + O_2(g)

e) Pb²⁺_(aq) +2Cl ^- --> PbCl_2(s)

02)  (UFJF) Na obtenção industrial do ácido nítrico é utilizado o processo de Ostwald, no qual a última etapa envolve a reação:

     3 NO_2(g) + H₂O_(l)   -->   2HNO_3(aq.) + NO_(g)

Assinale a alternativa incorreta:

a)      esta é uma reação de oxi-redução;

b)      nesta reação, a água é agente oxidante;

c)      o NO₂ é um óxido ácido;

d)      o ácido nítrico é um monoácido;

e)      o NO é um óxido neutro.

03)  (PUC-MG/JUNHO) Um dos métodos empregados para remover a cor escura da superfície de objetos de prata consiste em envolvê-los em folha de alumínio e mergulhar o sistema am água fervente com sabão de coco (meio básico). A equação que representa a reação é:

     Al_(s) + Ag₂S_(s)  Al⁺³_(aq) + S^-2_(aq) + Agº_(s)

Em relação à transformação ocorrida, assinale a afirmativa INCORRETA:
a) O alumínio sofre oxidação e, portanto, é o agente redutor.
b) O composto Ag₂S é o agente oxidante, pois contém o elemento prata (Ag) que provoca a oxidação.
c) A soma dos coeficientes mínimos e inteiros das espécies químicas, após o balanceamento da equação, é igual a 16.
d) O número de oxidação do Al varia de 0 para +3 no processo.
e) A prata doa elétrons, e seu número de oxidação passa de +1 para 0.

04) (FUNREI) Com relação à reação Zn + HgSO₄   -->   ZnSO₄ + Hg, qual é a afirmativa INCORRETA?
a) A reação é do tipo oxirredução.

b) O zinco foi o agente redutor.

c) O número de oxidação do enxofre não variou.

d) O mercúrio se oxidou pela ação do zinco.

05) (FADI-UBÁ) Introduzindo uma chapinha de cobre no ácido nítrico concentrado, ocorre uma reação química evidenciada pela liberação de um gás castanho e pela oxidação do Cu (cobre). Todas afirmativas baseadas ao texto são verdadeiras, EXCETO:
a) a coloração azul da solução evidencia os íons cobre.

b) ocorreu no frasco uma reação de decomposição do cobre.

c) a chapa de cobre diminui de tamanho.

d) ocorreu no frasco uma reação de oxi-redução.

06) (FADI-UBÁ) As roupas coloridas podem ser desbotadas quando usamos uma solução aquosa de NaClO (hipoclorito de sódio) conhecido comercialmente como água sanitária. A análise de alguns íons clorados mostrou para o cloro uma variação do estado de oxidação. Tais fatos nos permitem concluir que:
a) o cloro sofreu uma oxidação.

b) o cloro sofreu uma redução.

c) ocorreu uma reação de neutralização ácido-base.

d) ocorreu uma reação de oxi-redução.

07) (UFV) Considere as seguintes equações:
I - HCl + NaOH -->   NaCl + H₂O.

II - H₂ + 1/2 O₂ -->  H₂O.

III - SO₃ + H₂O  -->  H₂SO₄.

Ocorre oxirredução apenas em:

a) I.                              d) I e III.

b) II.                             e) II e III.

c) III.

08) (UFV-96) O permanganato de potássio (KmnO₄) pode ser obtido a partir do minério conhecido como pirolusita (MnO₂). As reações envolvidas no processo são:
2MnO₂ + 4KOH + O₂ --> 2K₂MnO₄ + 2H₂O
2K₂MnO₄ + Cl₂ --> 2KmnO₄ + 2KCl

Assinale a afirmativa CORRETA:

a)      MnO₂ e Cl₂ atuam como agentes redutores.

b)      KOH e K₂MnO₄ atuam como agentes redutores.

c)      K₂MnO₄ e O₂ atuam como agentes oxidantes.

d)      KOH e O₂ atuam como agentes oxidantes.

e)      O₂ e Cl₂ atuam como agentes oxidante

09)  (PUC-RIO 2008)

O fenômeno da oxirredução ocorre em reações com transferência de elétrons. Sobre a reação do permanganato de potássio com peróxido de hidrogênio em meio ácido, representada pela equação não balanceada abaixo, uma espécie doa elétrons, e a outra recebe esses elétrons de maneira espontânea, o que pode ser verificado pela variação do número de oxidação.

Sobre essa reação, é correto afirmar que:

       a)      o manganês no permanganato de potássio tem Nox 5+.

       b)      permanganato de potássio é a substância oxidante.

       c)      ácido sulfúrico é o agente redutor.

       d)      o oxigênio no peróxido de hidrogênio tem Nox médio 1+.

       e)      peróxido de hidrogênio é a substância que sofre redução.

---

10) (FUVEST 2010)

Na produção de combustível nuclear, o trióxido de urânio é transformado no hexafluoreto de urânio, como representado pelas equações químicas:

Sobre tais transformações, pode-se afirmar, corretamente, que ocorre oxirredução apenas em:

     a)      I.

     b)      II.

     c)      III.

     d)      I e II.

     e)      I e III.

11)  (UDESC 2010)

Abaixo são dados os potenciais padrões de redução dos metais prata e ferro, a 25 ºC.

Coloca-se uma barra de prata em uma solução aquosa de FeSO₄ 1,0 mol.L^-1, a 25 ºC. Com relação ao que deve ocorrer com o sistema acima, pode-se afirmar que:

a)                                a equação global da reação é: 

b)                                a barra de prata deve reagir com o FeSO₄

c)                                o FeSO₄ deve favorecer a oxidação da prata pela água em presença de oxigênio.

d)                                sendo a diferença de potencial igual a -0,36V, nas condições padrões a reação é espontânea.

e)                                sendo a diferença de potencial –1,24 V, nas condições padrões, nenhuma reação deve ocorrer.

12) (FUVEST 2009)

A pólvora é o explosivo mais antigo conhecido pela humanidade. Consiste na mistura de nitrato de potássio, enxofre e carvão. Na explosão, ocorre uma reação de oxirredução, formando-se sulfato de potássio, dióxido de carbono e nitrogênio molecular. Nessa transformação, o elemento que sofre maior variação de número de oxidação é o:

     a)      Carbono.

     b)      Enxofre.

     c)      Nitrogênio.

     d)      Oxigênio.

    e)      Potássio.

13) (UFPB 2009)

(Adaptado)

3CH₃CH₂OH + 2K₂Cr₂O₇ + 8H₂SO₄ →  3CH₃COOH + 2Cr₂(SO₄)₃ + 2K₂SO₄ + 11H₂O

Na reação acima, as substâncias oxidante e redutora são respectivamente:

     a)      K₂Cr₂O₇ e CH₃CH₂OH

     b)      CH₃COOH e K₂Cr₂O₇

     c)      CH₃COOH e H₂SO₄

     d)      K₂Cr₂O₇ e CH₃COOH

     e)      H₂SO₄ e CH₃COOH

01)       d

02)       b

03)       e

04)       d

05)       b

06)       d

07)       b

08)       e

09)       b

10)       e

11)       e

12)       b

13)       a